HashMap是根据key的hash值决策key放入到哪个桶(bucket)中,通过 tab=[(n – 1) & hash] 公式计算得出,其中tab是一个哈希表。
1. 为什么要保证 capacity 是2的次幂呢?
1)在get方法实现中,实际上是匹配链表中的 Node[] tab 中的数据。
(n – 1) & hash实际上是计算出 key 在 tab 中索引位置,当key的hash没有冲突时,key在HashMap存储的位置就是匹配的node中的第一个节点。如果hash有冲突,就会在node里面节点中查询,直至匹配到相等的key。
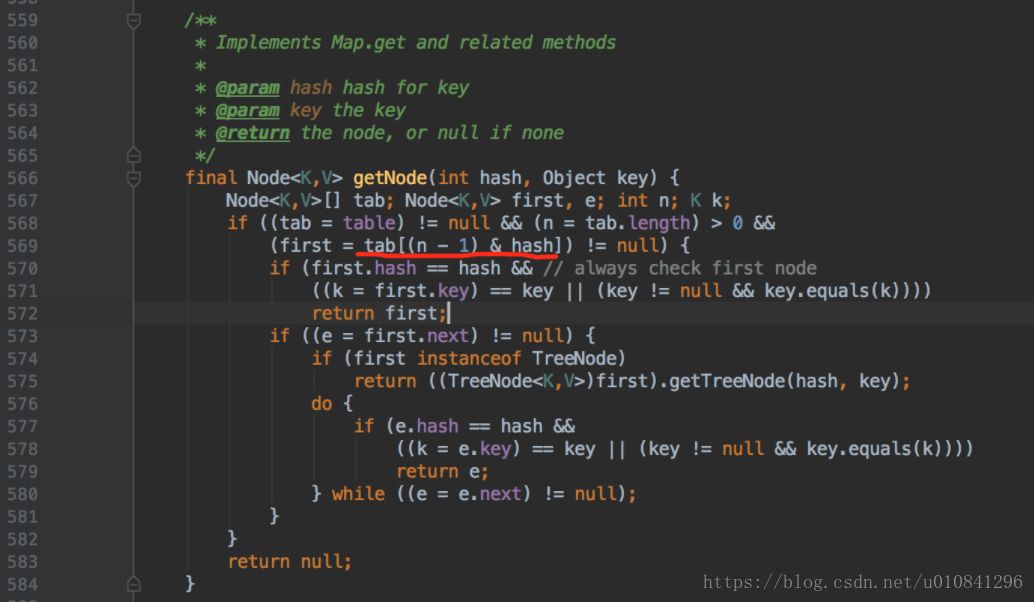
2)因为 n 永远是2的次幂,所以 n-1 通过 二进制表示,永远都是尾端以连续1的形式表示(00001111,00000011)
当(n – 1) 和 hash 做与运算时,会保留hash中 后 x 位的 1
例如 00001111 & 10000011 = 00000011
这样做有2个好处
-
&运算速度快,至少比%取模运算块
-
能保证 索引值 肯定在 capacity 中,不会超出数组长度
-
(n – 1) & hash,当n为2次幂时,会满足一个公式:(n – 1) & hash = hash % n
2.为什么要通过 (n – 1) & hash 决定桶的索引呢?
1)key具体应该在哪个桶中,肯定要和key挂钩的,HashMap顾名思义就是通过hash算法高效的把存储的数据查询出来,所以HashMap的所有get 和 set 的操作都和hash相关。
2)既然是通过hash的方式,那么不可避免的会出现hash冲突的场景。hash冲突就是指 2个key 通过hash算法得出的哈希值是相等的。hash冲突是不可避免的,所以如何尽量避免hash冲突,或者在hash冲突时如何高效定位到数据的真实存储位置就是HashMap中最核心的部分。
3)首先要提的一点是 HashMap中 capacity 可以在构造函数中指定,如果不指定默认是2 的 (n = 4) 次方,即16。
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
4)HashMap中的hash也做了比较特别的处理,(h = key.hashCode()) ^ (h >>> 16)。
先获得key的hashCode的值 h,然后 h 和 h右移16位 做异或运算。
实质上是把一个数的低16位与他的高16位做异或运算,因为在前面 (n – 1) & hash 的计算中,hash变量只有末x位会参与到运算。使高16位也参与到hash的运算能减少冲突。
例如1000000的二进制是
00000000 00001111 01000010 01000000
右移16位:
00000000 00000000 00000000 00001111
异或
00000000 00001111 01000010 01001111
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
3.capacity 永远都是 2 次幂,那么如果我们指定 initialCapacity 不为 2次幂时呢,是不是就破坏了这个规则?
答案是:不会的,HashMap 的tableSizeFor方法做了处理,能保证n永远都是2次幂。
/**
* Returns a power of two size for the given target capacity.
*/
static final int tableSizeFor(int cap) {
//cap-1后,n的二进制最右一位肯定和cap的最右一位不同,即一个为0,一个为1,例如cap=17(00010001),n=cap-1=16(00010000)
int n = cap - 1;
//n = (00010000 | 00001000) = 00011000
n |= n >>> 1;
//n = (00011000 | 00000110) = 00011110
n |= n >>> 2;
//n = (00011110 | 00000001) = 00011111
n |= n >>> 4;
//n = (00011111 | 00000000) = 00011111
n |= n >>> 8;
//n = (00011111 | 00000000) = 00011111
n |= n >>> 16;
//n = 00011111 = 31
//n = 31 + 1 = 32, 即最终的cap = 32 = 2 的 (n=5)次方
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
来源:https://blog.csdn.net/u010841296/article/details/82832166
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。